今回は、作成した卓球の球の軌道シミュレーターでどのような計算式を用いたか、解説していきます。内容的にはかなり複雑で、マニア向けになります。
シミュレーターは↓こちら。
基本的な物理量
| 物理量(定数) | 記号 | 値 [単位] |
| 球の質量 | m | 0.0027 [kg] |
| 球の直径 | d | 0.04 [m] |
| 重力加速度 | g | 9.8 [m/s2] |
| 空気の密度 | ρ | 1.204 [kg/m3]※1 |
| 空気の粘性率 | η | 1.82 × 10-5 [kg/(m・s)]※2 |
| 物理量(入力) | 記号 | [単位] |
| 初速度 | v | [m/s] |
| 発射角度 | θ | [度] |
| 回転数 | n | [回/s] |
※1…20℃、湿度0%、1気圧での値[1]
※2…20℃での値[1]
球に作用する力の大きさと向き
飛んでいる球に作用する力は以下の3つです。
- 重力
- 空気抵抗
- マグヌス力
これらについての基本的なことは、以下の記事でご説明しています。
それぞれの力の大きさについては、以下のように数値化しました。
1.重力
重力の大きさ
重力は高校物理を学んだ方にはおなじみの、[球の質量]×[重力加速度]mgです。これは球の速さや回転によらず、一定です。
重力の向き
y軸方向のみにはたらきます。球の飛ぶ方向によらず、x軸方向への重力は常にゼロ。
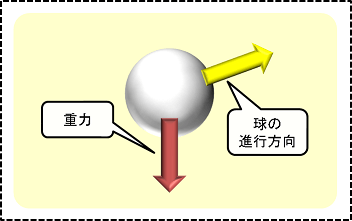
2.空気抵抗
空気抵抗の大きさ
物体が空気中を通過するときに発生する空気抵抗にはストークスの法則によるものとニュートンの法則によるものの2種類がありますが、前者は微小粒子に適用される法則なので、ここでは除外して考えます。
ニュートンの法則による空気抵抗Fdは、文献[3]より以下の式を用いて算出しています。速度の2乗に比例した抵抗を受けています。
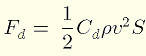
Cd…抗力係数
ρ…空気の密度
v…球の速度
S…球の断面積
Cdはレイノルズ数Reによって決まる係数で、今回のシミュレーションの範囲内では大体0.4~0.5程度に収まりますが、文献[4]にフィッティングされた式が紹介されているので、これを採用しました。
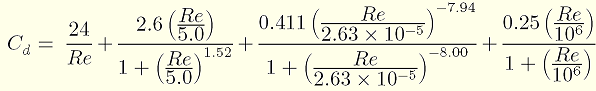
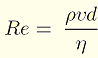
ρ…空気の密度
v…球の進行速度
d…球の直径
η…空気の粘性率
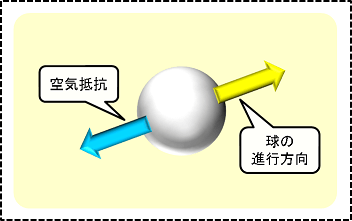
空気抵抗の向き
下図のように、球の進行方向と逆の方向にかかります。
3.マグヌス力
マグヌス力の大きさ
マグヌス力の大きさFLについては、クッタ=ジューコフスキーの定理[2]というものがあるらしく、以下のように与えられています。球の速さや回転数などの影響を受けます。
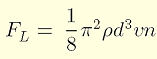
ρ…空気の密度
d…球の直径
v…球の進行速度
n…球の回転数
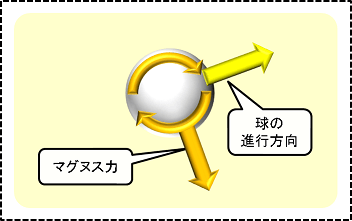
マグヌス力の向き
マグヌス力の向きは、球の前面が回転している方向にかかります。ドライブ系の球であれば主に下方向に、カット系の球であれば主に上方向に力がかかります。下図はドライブ回転の場合です。
4.まとめ
これらの力をx軸方向とy軸方向に分解し、それぞれの力の和を計算します。
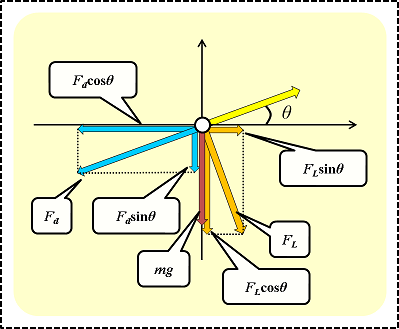
x軸方向…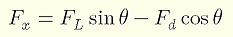
y軸方向…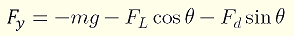
その後、微小時間経過後の速度と位置を算出。
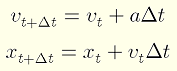
※F=maより、a=F/m
算出した速度を用いて、微小時間経過後の力の和を再計算、と繰り返していきました。
その他の要素
回転の減衰
回転の減衰に関して定式化されたものは見つけられなかったので(あるかもしれないけど)、文献[5]の実験データからおおよその減衰率を算出し、推定することにしました。今までの緻密な数式とは裏腹に、ここはかなり大雑把です。
実験データでは1秒間で大体10%~30%程度の回転の減衰が観察されていました。条件別で一定の傾向はみられたものの、データの性質上、定式化するのは難しそうだったため、ここでは一律で秒間20%の回転の減衰を想定することとしました。
実際のシミュレーションでは0.01秒刻みで計算しているため、毎回の計算で回転数に0.998を乗じています。
その他ofその他
マニアの方はこのページでの記載事項について、フォントが統一されていないことや数式を画像で貼っていることなどが気になることと思いますが、この辺はもう少しweb上での数式表現について統一化が進んだら修正しようと思っています。
ご理解くださりますよう、お願いいたします。
参考資料
[1] 理科年表2019 国立天文台編 丸善出版
[2] 法則の事典 山崎昶 朝倉書店
[3] 物理データ辞典 (社)日本物理学会 朝倉書店
[4] Data Correlation for Drag Coefficient for Sphere, Faith A. Morrison, 2016
[5] 卓球ボールの飛行中における回転数の変化について 上島慶ら 新潟体育学研究 2014


