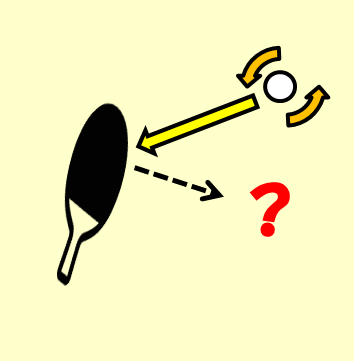
いよいよ、球の回転を考慮に入れた跳ね返りについて見ていきます。
早く実践的な話を聞きたいという方にとっては、鏡面反射と反発係数の話などは退屈なページだったかもしれません。
なお、ここでは裏ソフトラバーを前提として話を進めていきます。表ソフトラバーは、原則は同じですが回転の影響を低く見積もる(相手の回転の影響を受けにくく、自分から回転をかけにくいことを考慮する)必要があり、粒高ラバーについては法則自体が当てはまらない場合が多いのでご注意ください。
回転(摩擦)のある場合、ない場合
回転なし
まずは回転がない場合のおさらいです。鏡面反射と反発係数で扱いました。
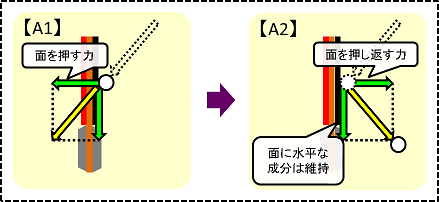
- 垂直方向にかかる力
- 水平方向にかかる力
→【A1】ラケット面を押す力が【A2】面を押し返す力になります。
→そのまま維持されます。
参考記事:ベクトルの合成と分解
回転あり
これに対して、回転がある場合を表した図が、以下です。
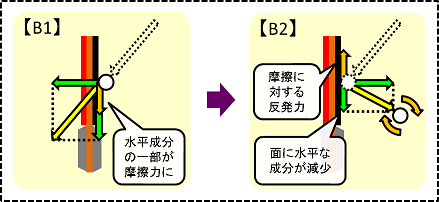
- 垂直方向にかかる力
- 水平方向にかかる力
→回転のない場合と同様です。
→【B1】一部が摩擦力となり、【B2】その反発力によって球が回転します。
ラケットに対して水平方向にかかる力が回転に変換される原理は、以下の記事で書いたとおりです。
当サイトでは、「球の表面すれすれをデコピンするイメージ」で解説しました。
参考記事:モーメントと球の回転
実例
この「斜めに進入してきた球が、回転しながらより面に垂直な向きに飛んで行く」現象。
卓球経験者であれば、試合でサーブを打つ前に癖でやっている方も多いのではないでしょうか。
「ラケットを地面と水平近くに保った状態で、斜めから球をぶつけて回転させつつ、垂直方向に飛ばす」
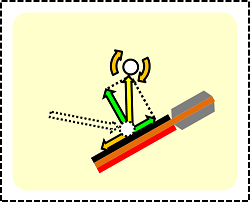
上図は【B2】の図を90度近く回転させただけですが、これでピンときた方もいるかと思います。(グリップの位置がおかしいのは、気にしないでください)
トッププロの選手でも、松平健太選手あたりがよくやっている印象があります。無回転の球をぶつけて回転に転換されるときの感触などを確かめているのですね。
まとめ
ここまでで、打球時にかかる基本的な力についてはひと通り押さえられたかなと思います。
当サイトではこれらの知識をもとに、いろいろな打ち方の技術や感覚論その他について検証していきたいと思います。
追記
※当サイトのベクトル表記は、基本的には「速さのベクトル」なのですが、今回の記事は表現の都合(摩擦力など)により、「力のベクトル」を中心に解説しています。
基本的に力と速さは比例関係にはないにしろ、相関関係があります。また、当サイトではそんなに厳密な部分まで計算する気がないです(というか、ラケットやラバーの種類等により、反発係数や摩擦力は異なるはずなので、一個人が踏み込める領域ではないと思っているのと、そこまでの情報を求めている人ってほとんどいないと思うので)。ですので、ベクトル表記が「力」だったり「速さ」だったりしますが、あまり気にしないでください。
当サイトは原理原則には踏み込みつつも、細かい部分まで深入りはしないスタンスで書いております。ご理解をお願いいたします。
ちなみに、比例関係と相関関係については、ざっくりと以下のような認識で書いています。
- 比例関係=力が2倍になれば速さも2倍になる
- 相関関係=力が大きくなれば速さも速くなる(等倍とは限らない)