ベクトルの合成と分解 | 卓球の物理学[pp-physics.com]

ここではベクトルの合成と分解について見ていきます。卓球の球の飛び方を把握する上で、避けて通れない考え方です。

ベクトルの合成

ふたつの異なる向きを持つベクトルが同じ物体に作用したとき、どうなるでしょうか。ここでは一例として、卓球のラケットとボールで考えてみましょう。
回転などの複雑な影響は除き、純粋に「ラケットを振る方向」と「ボールの飛ぶ方向」の2つのみを考えます。

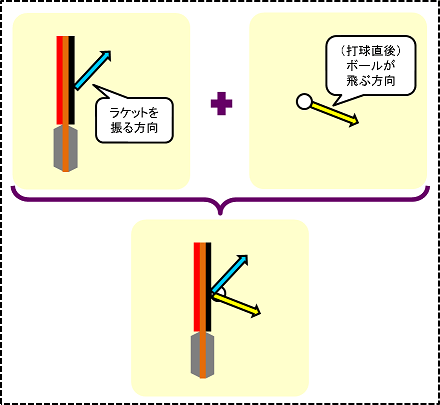
すると、ボールに対して2つの方向にベクトルが向いているのが分かります。この2つの力を受けたときに、最終的にボールの飛んで行く方向を図示すると、

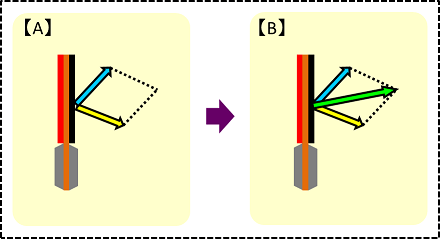
【A】それぞれのベクトルを2辺とした平行四辺形を作る（2つの補助線）
【B】補助線の交わった点に向けて、新しいベクトルを引っ張る

このようになります。

以下に、場合別で合成ベクトルがどうなるかを図示しました。

【C】ラケットの振りがより速かった場合
【D】ボールのスピードがより速かった場合

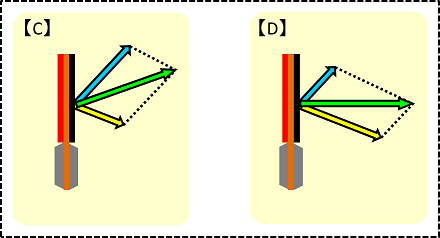
それぞれ、より速い成分の影響を受けていることが分かると思います。

時々、感覚論で「相手の打球の回転を自分の回転で上書きする」みたいな話があります。そのひとつの答えが、ここに関連していると思います。
自分のスイングスピードが速ければ、それだけ他のベクトルの向きの影響を無視できるようになります。
逆に、ボールの威力に負けてしまうと、同じようにラケットを振っていても思ったところに飛ばないといったことが起こり得ます。

ベクトルの分解

鏡面反射と反発係数の記事で少し触れましたが、ある面に対してかかる力はその面に垂直な力と水平な力に分けられます。

ここでは卓球において、ボールがラケットに当たる瞬間の力を分解してみます。

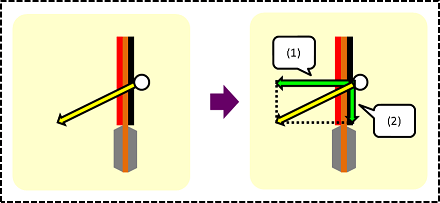
(1)垂直な力はラケットの面をガッツリ押す力
(2)水平な力は（摩擦がなければ）特にラケット面に影響を与えない力

先ほどの「ベクトルの合成」と逆の作業です。ラケット面に垂直な方向と水平な方向に補助線を引き、元のベクトルが対角線となるような長方形を作るイメージで分解します。
（先ほどのように平行四辺形にならないのは、ベクトルの分解方向が「垂直」「水平」と決まっていて、その2つの成分が直角だからです）

この作業はかなり重要です。ラケットに垂直な力に対しては、それを押し返す力が発生しますが、水平な力に対してはそれが発生しません。

「ラケットに厚く当てるか薄く当てるか」という部分とも深い関わりがあります。
厚く当てればスマッシュ系、薄く当てればドライブ系の打球になります。