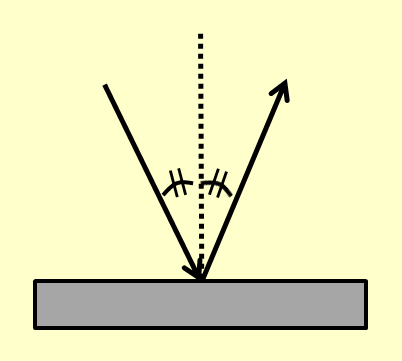
鏡面反射
読んで字のごとく、鏡のような平面に光などを当てたときの反射のことです。
下図のように、一定の角度で入射してきた光は別の方向に反射します。その際、反射の法則にしたがって入射角と反射角が同じ角度になります。
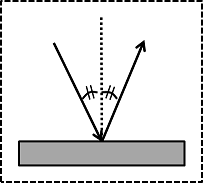
基本的には光だけでなく、ボールなどの物体も同じように法則が適用されます。
ボールを地面にバウンドさせることを考えた場合、実際には重力の影響でバウンドするまでに多少のカーブを描きます。
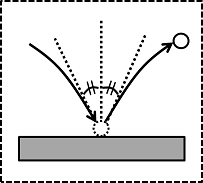
ここでの入射角はバウンドする直前のボールの進行方向によって決まります。つまりこれは、ボールの軌道上にあるバウンド直前のボールに対して引ける接線の方向ですね。

上の話はあくまで摩擦力や力の吸収などのない、理想状態での話になります。ここを出発点として、いろいろな要素を加味していかなければなりません。
反発係数
反発係数について
まずは反発係数(はねかえり係数)です。
現実世界ではある場所からボールを自然に落下させても、そのボールがバウンドして元の高さまで戻ってくることはありません。
バウンドしたときにボールの持つエネルギーの一部が失われてしまうからです(音とか熱とかになる)。
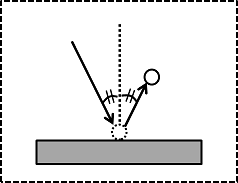
反発係数と卓球
卓球の球の反発係数は、標準的な裏ソフトラバーであれば大体0.7前後になるという実験結果があります(球速にもよりますが)。
詳しい式は割愛しますが、これはある高さから落下させた球を静止したラケットに当てた場合、最初の高さの半分ぐらいまで跳ね上がるという計算になります。
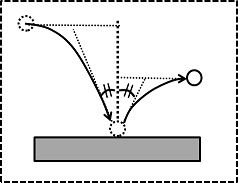
よく、ラケットやラバーなどの用具を選ぶときに、
「このラバーは跳ねないのでカットが安定する」
などと言うことがあると思います。
これは物理学的に言うならば、反発係数が高いか低いか、という話なのですね。
ちなみに、先ほどの図に付け加えると、高さ方向のエネルギーは表面との反発時のエネルギー吸収によって失われますが、水平方向のエネルギーは表面との摩擦によって失われます。
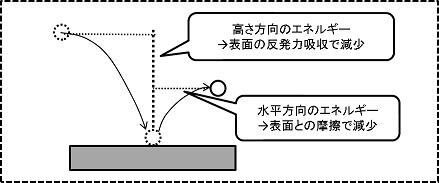
水平方向の摩擦のかかり方は、球のスピードや入射角、表面の種類などによって変わります。ラバーに対しては大きな摩擦が、卓球台に対しても少しだけ摩擦が発生します。
特に卓球で使用する裏ソフトラバーでは、水平方向のエネルギーの多く(ほとんど?)が回転エネルギーに変換されてしまいます。そこが卓球のいちばんの特徴ではないでしょうか。
特に卓球の主要技術である「ドライブ」を考える上では、この水平方向の摩擦力がキモです。この辺りは当サイトでもいろいろと分析しておりますので、興味があったらご覧になってください。