球の反発方向の決まり方

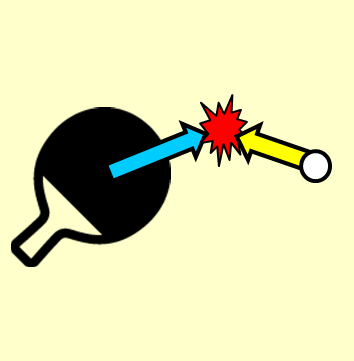
ベクトルの合成と分解の記事で、

の2つのベクトルの合成について書きました。

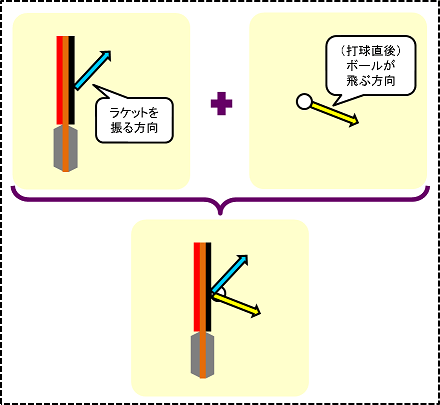
このうちラケットを振る方向はいいとして、打球の飛ぶ方向がどのように決まるのか？
ここではそれを考えていきたいと思います。
（なお、ここでは摩擦・回転の影響は考えておりません）

球の反発方向

ラケットを振らない場合

これはシンプルに鏡面反射の法則にしたがいます。

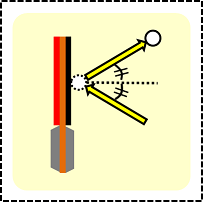
参考記事：鏡面反射と反発係数

ラケットを振った場合

それでは、以下のような場合はどうでしょうか。

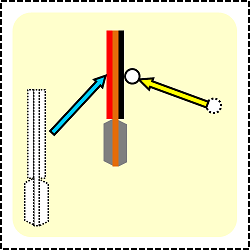
まずは、それぞれのベクトルの分解を行います。そして出てきたベクトルにそれぞれ番号をふります。

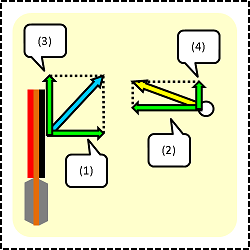
ここでちょっと変なことをイメージしていただきたいのですが、

ラケットが巨大化して自分がその上に乗っていると考えてみてください。
は？何言ってんの？と思うかもしれませんが

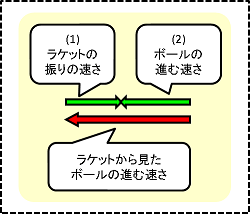
自分は(1)の速さで右に進んでいます。そこに(2)の速さでボールが飛んできました。
すると、ラケットの上の自分としては、(1)と(2)を足した速さでボールが迫ってくるように感じますよね？

車に乗って進んでいて、対向車が迫ってくるときの感覚と似ています。信号待ちをしているときに迫ってくる対向車と比べると、かなり速く感じるのと同じです。

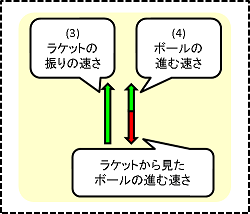
次に、(3)と(4)についても見てみましょう。

この場合、ラケットもボールも上方向に動いていますが、そのスピードはラケットの方が速いです。
なので、ラケットの上の自分としては、むしろボールが下に向かって動いているように感じます。

これも車で例えます。高速道路を並んで走っている車をイメージしてください。
自分の乗っている車の方が少しスピードを出していると、並走している車も前に向かって進んでいるのにちょっとずつ後ろに下がっているように見えますよね。

あれと同じで、上図のラケットから見ると、ボールは少し下方向に向かって動いているように見えるのです。

以上より、ラケットの上にいる人から見たボールのベクトルは、それぞれの赤いベクトルを合成した、以下の黄色いベクトルになります。

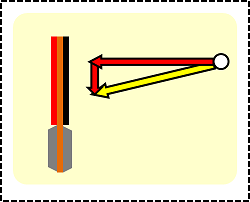
ラケットの上の人からすると、動いているのは周りの世界であって、まさか自分の乗っているラケットが動いているとは思っていません。地球が動いているように感じられない私たちと同じです。上図はそんな人たちから見たボールのベクトルです。

さて、ここまでの話は見る人の視点が変わっただけであって、ラケットやボールのもともとのベクトルの速さや向きが変わったわけではありません。

以下の図で、

この【A】と【B】は視点が違うだけで、同じ世界の出来事なのです。

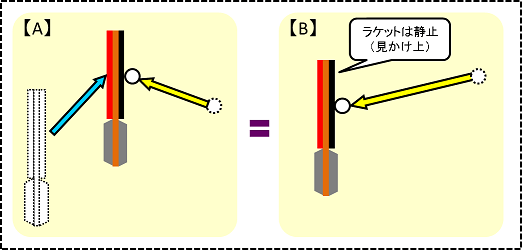
つまり、この問題は右側の図をもとに考えても良いということになります。そして、右側の図の方がラケットが（見かけ上）静止している分、単純です。冒頭で出てきた「鏡面反射」の問題と同じ条件だからです。

この場合、ボールは黄色いベクトルの方向へ打ち出されます（反発係数を考慮して、矢印を少し短めにしています）。

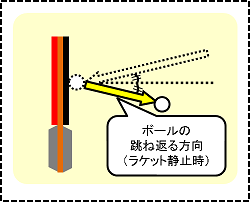
ただし、これはラケットが静止している場合であって、実際にはラケットを振っているので、その分のベクトルを合成しなければなりません。

最終的には、このようにボールが飛んでいきます。

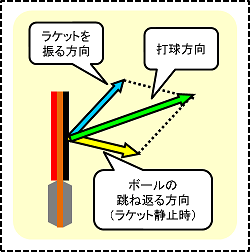
まとめ

いかがでしたでしょうか。難しくて、1回読んだだけでは理解できないという方も多いのではないかと思います。
（私も理解するまでに結構時間をかけました）

そんな中で、大変残念なお知らせなのですが…

既に結構複雑なのに、ここまでの話にはまだ「回転」の話が一切出てきていないのです。そう、卓球のいちばんのキモである「回転」の話が。

回転の力を加えると、ここからまたさらに複雑な話になります。その辺は、別記事にて扱っていきたいと思います。