ベクトルと接線

卓球の物理学を理解するにあたって、まず基本的な考え方として「ベクトル」と「接線」についての理解が必要です。
（接線は、分からなくてもいいかも）

両方とも知っているという方は、本記事は飛ばしていただいてかまいません。

ベクトルと卓球

ベクトルとは？

ベクトルとは【大きさ】と【向き】を持つ量のことです。

例えば、物を動かそうとする「力」には、
【大きさ】…どれだけの力をかけるか
【向き】…どの方向に力をかけるか（押す、引くなど）
の2つがあります。

当サイトで扱うベクトルは「速さ」のベクトルになります。「速さ」にも【大きさ】と【向き】がありますよね。

以降、当サイトで表されるベクトルは特別な断りのない限り「速さのベクトル」を表します。

ベクトルの表記

ベクトルは矢印で表すことができ、

をそれぞれ示しています。

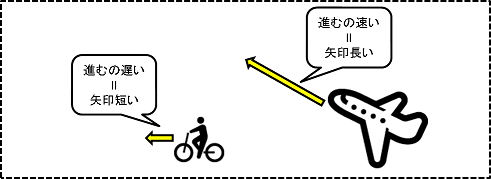
卓球におけるベクトル表記

卓球でも同じように考えます。【大きさ】については、例えばストップした打球とスマッシュした打球では速さが明らかに違います。これを矢印の長い短いで表すわけですね。

ストップの場合

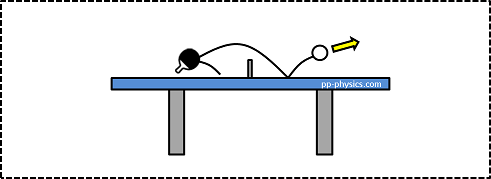
スマッシュの場合

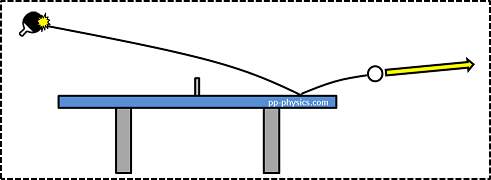
ただ、この表し方だと「あれ？この先、ボールがこの矢印の方向に一直線に進んでいくのかな？」と感じてしまうかもしれません。

実際にはボールは重力などの影響を受けて、時々刻々と進む【向き】が変わります。
難しい説明をしなくても直感的に分かるかと思いますが、例えば以下の図のように、バウンド直後なら右上方向(1)、頂点では純粋に右方向(2)、そこから先は右下方向(3)にボールが進んでいきます。

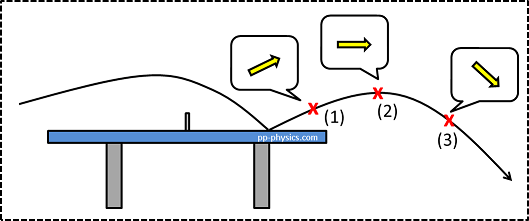
つまり、卓球の球に対してこの矢印が書かれていた場合、その矢印はその位置にある球の状態のみを表しているということになります。ちょっと進めば球の威力も落ちますし、進む向きも変わるわけですから。

そのことを理論的に理解するために必要なのが「接線」の考え方です。
（逆に言えば、上の図の意味が分かれば、あえて理論的な部分を理解する必要はないかもしれません）

接線と卓球

接線とは？

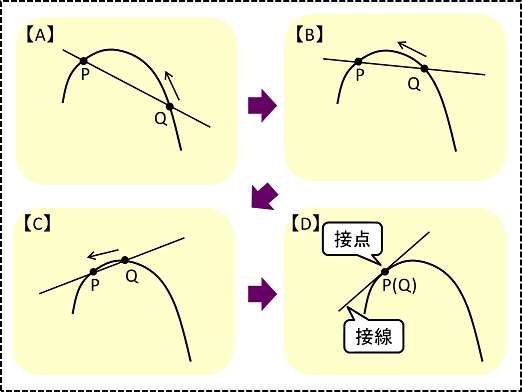
以下の図で、接線について考えてみます。

この重なったときに引かれた線が接線で、重なった点P(=Q)が接点です。

卓球における接線と接点

仮にこの曲線が卓球の球の軌跡であり、接点の位置に球があるとすると、そのときの球の進行方向は接線方向になります。

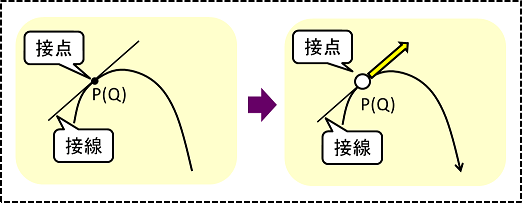
卓球の球の位置（接点の位置）が変われば球の進行方向（接線方向）も変わることがお分かりいただければと思います。